10+9+8*7*6*5+4+321

Happy New Year!

First digits after the decimal point

Éric Angelini is not at the moment updating his latest sequence suggestion, so I will post my extension (assuming a 1, 2 start) here:

1, 2, 11, 5, 42, 4, 94, 7, 74, 20, 27, 129, 101, 777, 7618, 1124, 14753, 1218, 82554, 8156, 98795, 3206, 32451, 499, 15377, 2366, 15386, 1868, 121402, 2419, 199254, 5819, 292038, 9247, 316636, 13812, 43621, 38327, 36725, 95818, 260900, 20134, 771711, 58457, 54269, 92835, 60177, 55065, 91504, 25771, 281635, 53566, 190196, 355062, 1866812, 199551, 10689395, 186879, 17482653, 95960, 54888692, 216986, 39532004, 138119, 34938527, 829143, 23731481, 189726, 7994697, 1908167, 23867906, 7480187, 31339937, 11404557, 36389852, 32664599, 23949435, 5535335, 23112591, 6504115, 6357184, 3851878, 6059094, 489221, 807416, 1650409, 2044061, 12385171, 10283218, 83028464, 807417055, 82135674, 101726454, 26620507, 261687159, 61339564, 2344003581, 48771083, 2080674423, 22994000, ...

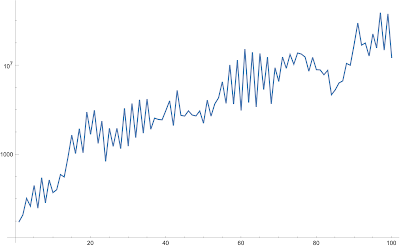click to enlarge

Dangerous obsession

wearing clogs on the stove and the countertop

A million-digit Leyland prime (third one)

After my second find, I really did not think that I would generate another example in my current search space. However, at the upper end of that space:

194968^136197+1*136197^194968 is 3-PRP!

This is now the 14th largest-known Leyland prime. Ryan Propper owns the largest 13:

19 million-digit Leyland primes (via Norman Luhn); n-th Leyland + 1 = A076980 index

Bucket list #1

My original five-piece bucket list is here with #2 here.

1. Wiener schnitzel (The Coffee Mill closed in 2014; Amber closed in 2021.)

Café Polonez: 195 Roncesvalles Ave

Catherine and I had lunch today at Café Polonez with Shelley and Denny Mylko. The restaurant is just north of Fern Ave. I of course had the pork schnitzel:

schnitzel with cole slaw, beets, carrots, and potatoes: $21.95 plus tax

Very nice!

Neheim-Hüsten street view

Three years ago I wrote an article about my Neheim birthhouse, captured from a distance on a bicycle-ride YouTube video. In it, I bemoaned the absence of Google's street view. Today, by chance, I noticed that Google has (from October 2022) a very limited street-view coverage of Neheim (and its 1950s-era twin town of Hüsten):

baby-blue roads have street view: click to enlarge

I was fortunate that my birthhouse was visible from Bergheimer Weg (in that 2009 blog post is a link to a 1934 photograph of the house being built):

Bergheimer Weg 16, October 2022

Swap

Éric Angelini's blog post last Friday (Underline, reproduce) motivated me to attempt to solve

S9 = ninth, twentieth, thirtieth, fourth, ninetieth, sixth, seventh, eighth, ...

... wondering how many swaps (of "first, second, third, fourth, fifth, sixth, seventh, eighth, ninth, tenth, eleventh, …") were needed to produce it. It stymied me for a day or so but (using a combination of manual and Mathematica step-throughs) I eventually got this:

S9 = ninth, twentieth, thirtieth, fourth, ninetieth; sixth, seventh, eighth, first, tenth, second, twelfth, fifteenth, thirtyeighth; thirteenth, fifth, eleventh, eighteenth, nineteenth, seventeenth, twentyfirst, twentysecond, fourteenth; twentyfourth, twentyfifth, twentysixth, twentyseventh, twentyeighth, sixteenth; third, thirtyfirst, thirtysecond, thirtythird, thirtyfourth, thirtyfifth, thirtysixth, thirtyseventh, twentythird; thirtyninth, fortieth, fortyfirst, fortysecond, twentyninth; fortyfourth, fortyfifth, fortysixth, fortyseventh, fortyeighth, fortyninth, fortythird; fiftyfirst, fiftysecond, fiftythird, fiftieth, fiftyfifth, fiftyfourth; fiftyseventh, fiftyeighth, fiftyninth, sixtieth, sixtyfirst; sixtysecond, sixtythird, sixtyfourth, sixtyfifth, fiftysixth; sixtyseventh, sixtyeighth, sixtyninth, seventieth, seventyfirst, seventysecond; seventythird, seventyfourth, seventyfifth, seventysixth, seventyseventh, seventyeighth, sixtysixth; eightieth, eightyfirst, eightysecond, eightythird, eightyfourth, eightyfifth, eightysixth, eightyseventh, seventyninth; eightyninth, eightyeighth, ninetyfirst, ninetysecond, ninetythird, ninetyfourth, ninetyfifth, ninetysixth, ninetyseventh, ninetyeighth, ninetyninth, onehundredth; ...

In case you are still wondering what this is all about, the sequence of written-out ordinals reproduces itself if you take its 9th, 20th, 30th, 4th, 90th; 6th, 7th, 8th, 1st, 10th, 2nd, 12th, 15th, 38th; 13th, etc. letters. I have replaced commas with semicolons where the spelling of each ordinal ends. The semicolon after "onehundredth" indicates the end of "thirtyeighth".

So I told Éric that there were 24 swaps, i.e. red-lettered ordinals (where the number does not correspond to its position in the sequence). But in my mind "swap" has a strong sense of pairwise exchanges, which is not the case here. There are three such pairwise exchanges: Positions 1 with 9, 3 with 30, and 13 with 15. But the rest are more involved. Position 14 goes to 38, which goes to 23 (which goes to 14). Position 2 goes to 20, which goes to 17, which goes to 11 (which goes to 2). Finally, position 5 goes to 90, which goes to 88, which goes to 79, which goes to 66, which goes to 56, which goes to 54, which goes to 50, which goes to 43, which goes to 29, which goes to 16 (which goes to 5).

Update: I've calculated 11001 indexed terms for

S10 = tenth, eighteenth, twentyeighth, ninetieth, fifth; second, seventh, eighth, ninth, first, sixth, eleventh, eleventhousandth, fourth, fifteenth; fourteenth, seventeenth, twelfth, third, sixteenth, twentyfirst, twentysecond, twentythird, twentyfourth, twentyfifth, twentieth, twentyseventh; ...

In the linked file, the 1098 red entries are indicated by an asterisk at the end of the line.

Man versus nature

two men with leaf blowers (across the street, last Thursday)

same driveway (left) this morning

Doctor in the Tardis

After a decade-long hiatus of not seeing my family doctor, on September 27 I had my first appointment with a new doctor. After taking down some of my personal information we agreed to my doing a blood test and an Ontario Health fecal immunochemical test. In an October 13 phone appointment, he relayed the bad news: My cholesterol was high, which when combined with my family history of stroke (my father had one) suggested medication. When I indicated reticence to go on meds he allowed me a three-month reprieve of diet and exercise followed by a retest. To add insult to injury, the fecal test proved abnormal, inviting a colonoscopy. I suggested that the result was a false positive based on contamination with hemorrhoidal bleeding.

So I spent a month researching the matter and, this afternoon, saw him in order to share my findings. I decided ahead of time not to get into the family-history-of-stroke matter which I saw as confirmation bias on his part (he didn't even know at what age my father had the stroke). The diet-and-exercise bit is of course something to be suggested regardless (as it is generally worthwhile), not as a designed-to-fail antidote to statins. I wasn't going to get into that either as it evidenced a desire to get me on meds and I didn't want to be confrontational. At any rate, the matter was moot as I had found sources that suggested (in the absence of cardiovascular disease, diabetes, etc.) that I had no need to be on meds.

First, I presented Dr. Ian Neeland's (22 Dec 2020) podcast quotation of "10 years on a statin with low LDL cholesterol might decrease your risk [of heart attack, stroke, etc.] by 20 percent" as being (for me) a negligible benefit. Next, I presented Robert M. Kaplan's (3 Apr 2019) opinion piece on preventing heart disease, starting with some absolute risk-of-dying meta-analysis statistics and concluding with "... observations on people over the age of 70 do not show any statistically significant statin-related reductions in deaths from any cause."

Throughout most of the session my doctor seemed overly defensive, mildly angry perhaps. He interrupted me several times, explained that he was following guidelines, and cautioned me on cherry-picking data. He closed the door to the hallway at one point. Much more was said but I choose here to be brief.

I had run out of my 15 minutes and I hadn't yet dealt with the fecal test. I asked for a couple more minutes. I explained my false-positive belief, suggested that it didn't matter anyways because I had "a very low long-term risk of colorectal cancer" based on a (19 Sep 2013) study on long-term colorectal-cancer incidence and mortality. I finished with Michael Bretthauer's "gold-standard trial" that had colonoscopies cutting cancer risk by only a fifth with no significant reduction in colon cancer mortality. How do you like them apples cherries?

New Jersey

Rogue Amoeba has updated their Audio Hijack to version 4.3 and I had been meaning to upgrade my 3.7 app for a while now. Tipping the scale was a "transcribe" block that I thought might prove interesting in attempting the lyrics to Dave Van Ronk's Garden State Stomp. There were two available options for the transcription: high accuracy which, in spite of the lengthy time that it took, proved abysmal, and low resources which, utilizing an AI-based Large Language Module, was just as bad, only with added nonsense.

Places per line are 4/4/12 (times 4 = 80). Lyrics/spelling as per the video:

Allamuchy, Hacklebarney, Rockaway, Piscataway.
Ho-Ho-Kus, Secaucus, Lower Squankum, Fair Play.
Wanamassa, Succasunna, Manumuskin, Plumbsock, Bivalve, Buckshutem,
  Turkey Foot, Macanippuck, Jugtown, Febletown, Nummytown, Rahway.

Wickatunk, Manunka Chunk, Mantua, Mizpah.
Manasquan, Raritan, Matawan, Totowa.
Whippany, Parsippany, Penny Pot, Hackensack, Batsto, Nesco,
  Metedeconk, Peapack, Loch Arbour, Egg Harbor, Swinesburg, Caviar.

Cheesequake, Boy Scout Lake, Moonachie, Tenafly.
Netcong, Watchung, Pluckemin, Mount Misery.
Bardonia, Ironia, Colonia, Weehawken, Manahawkin, Mantoloking,
  Mahalala, Pennsauken, Dutchtown*, Ironbound, Frelinghuysen, Lodi.

Hardscrabble, Double Trouble, Picatinny, Montague.
Muckshaw Pond, Ockanickon, Espanong, Ocean View.
Navesink, Shabakunk, Ongs Hat, Jumbo, Wortendyke, Water Witch,
  Blue Ball, Ringoes, Matchaponix, Delawanna, Wawayanda, Timbuctoo.

* which Van Ronk seems to pronounce Ducktown.

Bucket list #2

My original five-piece bucket list is here with #3 here.

2. China Town (Their online ordering system stopped working a few years ago.)

1790 Jane Street @ John Street

The picture is Google street view (July 2023). I did eventually find another website ordering system for them but I was reluctant to use it in case it was a scam. Researching the website provider (MealKeyway), I decided finally that it was ok.

3 large Beef Fried Rice (no onion) $22.47; Sweet & Sour Chicken Balls $11.99; Fried Mixed Vegetables (no onion) $9.99; there's a $40 minimum food-only order; tax $5.78; delivery $4.99; tip $3.00; rounding -$0.02: total $58.20

Pretty much the way I remembered it, although I used to get BBQ chicken wings as well. I hadn't before used a no-onion option on the mixed vegetables. They replaced it with more broccoli which (unfortunately) was excessively salty. I guess the florets/buds retain a lot of the briny broth. I can run them under the faucet in the leftover reheats.

Leaving

a tree shedding its leaves in the breeze

AD one billion

Éric Angelini's latest offering is based on the absolute differences (AD, be they odd or even) of an integer sequence's adjacent digits determining the sequence's new numbers. After Giorgos Kalogeropoulos posted one million terms, I struggled to better his (apparently Mathematica) result to five million terms before realizing that my one-at-a-time AppendTo approach was not the best tool for this game.

Starting with 315 terms of the sequence (s) we generate — in twelve steps — over one billion terms by repetitively determining the adjacent-digits sequence, creating therefrom an absolute differences sequence, and applying a sign change to those differences that are even. Prepend zero, Accumulate, add 10.

Table[d=Flatten[IntegerDigits[s]]; c=Abs[Most[d]-Rest[d]]; f=Prepend[Table[If[OddQ[c[[i]]],c[[i]],-c[[i]]], {i,Length[c]}], 0]; s=Accumulate[f]+10; Length[s], {12}]

{577, 1181, 2719, 6976, 19556, 57525, 203635, 791890, 3733165, 21270116, 140287834, 1002951921}

That's it! Truncate the final 1002951921 terms to 10^9 terms, take every tenth integer (Mathematica has trouble enough plotting 100 million points), and graph:

click to enlarge

Recycling

This is the sixth recycling bin put out for city collection containing mostly old journals and magazines. It was precipitated (literally) by the roof leak that meandered through an upstairs slanted ceiling closet I was using as storage space. Even though I am holding back on my most prized collections, I think it likely that I will contribute another six bins before I am done. Here's a photo of some of the "paper" that has (mostly) already gone:

Air show

Looking southeast from my back deck, I'm guessing these are the U.S. Navy Blue Angels.

A million-digit Leyland prime (encore)

Hot on the heels of my million-digit Leyland prime find, I have come across another one:

197180^119151+1*119151^197180 is 3-PRP!

This one was a little unexpected because it is so close in size to my other one, a mere five decimal digits less. The current top-five Leyland prime leaderboard now looks like this (the first column is the number of digits):

1717671  (1343238,19)      Ryan Propper    May 2023

1433792   (300102,59935)   Ryan Propper    May 2023

1268947  (1139148,13)      Ryan Propper    Jul 2023

1000910   (191319,170462)  Hans Havermann  Jul 2023

1000905   (197180,119151)  Hans Havermann  Aug 2023

833719/265381

Based on the simple continued fraction of π, its convergents (rational approximations) are: 3/1, 22/7, 333/106, 355/113, 103993/33102, 104348/33215, 208341/66317, 312689/99532, 833719/265381, 1146408/364913, ...

Prime numerators are at position 1, 5, 9, ... Prime denominators are at position 2, 4, 9, ... The ninth convergent therefore has both prime numerator and prime denominator, noted ~2003 in the OEIS. It seems unlikely that we will ever see another such.

I thought it might be useful to have here a listing of the positions of prime numerators (p/) and prime denominators (/p) so as to better assess the rarity of their confluence:

1/
/2
/4
5/
9/
/9
11/
16/
/33
87/
230/
334/
594/
/595
840/
853/
/1127
1149/
/2003
2726/
/3611
3788/
/4356
/6926
7442/
8751/
/25333
/27652
/32395
/37722
42038/
/114199
143753/
...

A million-digit Leyland prime (I got lucky)

Back in April, I wished myself "better luck" in my current million-digit Leyland prime search. I've won that lottery, so to speak:

191319^170462+1*170462^191319 is 3-PRP!

The number has 1000910 decimal digits. The current top-five Leyland prime leaderboard now looks like this (the first column is the number of digits):

1717671  (1343238,19)      Ryan Propper    May 2023
1433792   (300102,59935)   Ryan Propper    May 2023
1268947  (1139148,13)      Ryan Propper    Jul 2023
1000910   (191319,170462)  Hans Havermann  Jul 2023
1000175   (218767,37314)   Gabor Levai     Mar 2023

Trouble above

I noticed mid-June a stain on the ceiling of my main-floor library room, likely a consequence of the 30 mm precipitation received on June 12. It necessitated a new roof:

click to enlarge

Busy spell

kitchen @ 3:45 am: click to examine the chaos in greater detail

Goodbye landline

My brand new iPhone 13 arrived yesterday. I wasted little time in trudging up to Freedom Mobile (1924 Weston Rd.) in the heat — twice (I didn't bring any identification the first time)! So now I have a cellphone number. This meant that I could lose the "home" phone which I had been using only as a two-factor authentication device. When I called Bell, they dragged out the cancellation process and finally offered me the landline (I'm paying $60 per month) for something closer to $10 per month (if I heard correctly). "Just cancel the fucking phone," I blurted out uncharacteristically.

Shoe change

21 December 2014

14 June 2023

Little free library

Ross and Laurie (beside Denison Park at Lippincott) have set up this very nice "little free library" box in a corner of their place. I should be able to donate a few books from my own mostly-reference library. Not everyone thinks that these things are a good idea.

Agent orange

This late-evening marauder comes as close to being "orange" (especially in the tail) as one might deem possible. Close inspection suggests that the effect might just be a whitened mixture of "brown". A search finds that the descriptive word for it is "erythrism". This particular raccoon paced our back- and side-yards for a half-hour or so before finally climbing the fence into a neighbour's yard. This included ventures onto the back deck and peering into the kitchen door. When I went out in order to scare it away, it was somewhat unconcerned by my approach — perhaps even attracted to it — as though it was tame. This leads me to suppose that it might be suffering from distemper.

Update: Two days later it was on its way to be euthanized...

A million-digit Leyland prime (ryanp)

Ryan Propper ("ryanp" on Mersenne forum) had not contributed any Leyland primes prior to Wednesday, when he proclaimed this 1433792-digit integer to be a PRP. Then yesterday, he added another (at a mere 582101 digits) that had a small y [L(x,y) defines a Leyland integer as x^y+y^x, x≥y; here y=2]. The current top-five Leyland prime leaderboard now sports three million-digit Leyland primes (the first column is the number of digits):

1433792    (300102,59935)   Ryan Propper   May 2023

1000175    (218767,37314)   Gabor Levai    Mar 2023

1000027    (211185,54364)   Gabor Levai    May 2022

 582101   (1933695,2)       Ryan Propper   May 2023

 506429    (107890,49423)   Miklos Levai   Feb 2022

A million-digit Leyland prime (ramp-up)

This is an update to my previous "retry" post, wherein I announced a new million-digit Leyland prime search attempt. Today I finished ramping up the search from the initial 12 processes on 3 computers (covering 20% of the search space) to  57 processes on 18 computers (covering about 70% of the search space). My search last year had the same 18 machines doing 108 processes but I subsequently discovered that this overloading of processes was highly inefficient and detrimental to the effort. My current 57 processes should all be done (roughly) in early November and I can assign the remaining 30% of the search space — process by process, as they come due — at that time.

A million-digit Leyland prime (retry)

After my last disappointing attempt, I have started again today on a new search. Initially, I will commit twelve processes (on my fastest three computers) to about 20% of the search space, with a completion date of late October. I'm hoping for better luck this time around.

Bucket list #3

My original five-piece bucket list is here with #4 here.

3. KFC (It's a bucket list! Like Domino's Pizza, I've been unable to generate a delivery.)

1300 Weston Road

10-piece 'original' bucket; large fries, cole slaw, potato salad: $41.80, which included a $3
charge to guarantee 7 'white-meat' pieces, but I got only 6 (plus a drumstick and 3 wings)

All around my hat

It has been a long time since we were all excited by the aperiodic tilings of Penrose's kites and darts. There was even a version using images of chickens:

Penrose chickens

There is now a new tiling that reduces the number of necessary shapes from two to one, the first true aperiodic monotile:

Brad Klee: headliner

A million-digit Leyland prime (lghu)

Twenty-five days after I started my million-digit Leyland prime search last year, Gabor Levai — who goes by the handle "lghu" on Mersenne forum: small L, not capital i — discovered a 1000027-digit example that was in my purview.

He's done it again! This morning, eighteen days after I started my new run, Gabor posted a 1000175-digit, new prime that was in the range of Leyland number pairs I was prepared to look at this year. In fact, when I was sieving my pairs I had a choice of going low (1000100 digits up to 1000200 digits) or going higher (as high as 1000900 digits up to 1001000 digits) and I chose the lower range as I had convinced myself that Gabor was probably not engaged in a like-minded endeavour.

The advantage for me of going low is that my searching is exhaustive. Having already looked at all Leyland number pairs of 1000000 digits up to 1000100 digits, finding a new PRP in the range of 1000100 digits up to 1000200 digits would allow me to (eventually) say that that the new PRP and the previous 1000027-digit one are consecutive Leyland primes.

Update (March 15): I have ceased my new run on the understanding that Gabor will himself check all of the intervening Leyland candidate pairs for primality. Indications are that he can do this faster than I. Coincidentally, I found a new 386805-digit prime early this morning, the first such since 2 May 2022.

A million-digit Leyland prime (start of a new run)

Five days ago I started a new run of testing candidates for the property of being a million-digit Leyland prime. The million-digit part is relatively easy; the primality testing, not so much. My last run required nine months, not counting the month it took to sieve. I'm not pushing it for now. Of the 59364 candidates in this run, I'm only doing 9000 on my three iMacs. This should be done in July. My Mac minis are testing much smaller Leyland numbers (currently ~386750 digits) for primality and I'll keep that going until I exhaust my current crop of sieved numbers in that range. Only then will I divert them to help in the million-digit hunt.

Small-string final non-appearance coincidences in base-ten powers of two

If we look at OEIS A094776, one sees the beginnings of sequences that apply the inherent concept to strings of more than one digit. Keith Lynch suggested the idea (tongue-in-cheek, I thought) on MathFun a few days ago and Maximilian Hasler actually worked out the numbers for strings 10 to 18. I decided to chart a more comprehensive listing...

My results: sorted by strings and sorted by powers of two. There are "coincidences" where two or more strings share the same power of two as their final non-appearance exponent (for example, the two 71s in A094776 for digits 5 and 7). I'll list those here after brief summaries of each n-digit result:

1-digit strings

{71,5}
{71,7}
...
range: 119.5 ± 48.5
average: 1026/10
...
{153,3}
{168,2}

string coincidence

71: {5,7}

2-digit strings

{1300,91}
{1416,07}
...
range: 2399.5 ± 1099.5
average: 215386/100
...
{3493,28}
{3499,95}

string coincidence

2146: {33,48}

3-digit strings

{20589,141}
{20729,713}
...
range: 37290.5 ± 16701.5
average: 28860154/1000
...
{51375,552}
{53992,661}

string coincidences

22044: {024,275}
24486: {404,675}
25305: {410,947}
25440: {317,604}
25668: {442,815}
25704: {123,766}
25980: {096,868}
26046: {378,588}
26136: {422,677}
26316: {227,929}
26477: {152,690}
26695: {085,256}
26792: {048,732}
27003: {737,974}
27121: {545,932}
27479: {183,687}
28196: {300,554}
28252: {116,641}
28270: {099,575}
28317: {578,656}
28425: {287,392}
28532: {171,910}
28609: {017,919}
28784: {033,719}
28850: {164,647}
28891: {346,505}
29173: {648,787}
29705: {668,997}
29711: {335,799}
29976: {665,995}
30977: {131,395}
32637: {076,426}
33550: {555,796}
33607: {582,598}
33631: {117,735}
39571: {021,622}

4-digit strings

{266774,6355}

{273317,4949}

...

range: 459917 ± 193143

average: 3642758125/10000

...

{625874,6636}

{653060,6164}

string coincidences

296341: {0317,9730}

299582: {2041,2103}

302068: {8362,9844}

303160: {1883,2335}

304631: {5262,7194}

304639: {2896,5816}

305663: {5142,5397}

307552: {0904,8968}

307739: {9064,9656}

308220: {2396,6102}

308408: {5509,8025}

308917: {0658,5181}

309422: {2879,8852}

310452: {2800,6576}

310789: {0093,5900}

311943: {4436,7337}

312480: {5954,9044}

312956: {1741,1944}

313628: {7855,9582}

314127: {4003,6689}

315423: {6059,6252}

315844: {3119,7155}

316864: {2825,4655}

317042: {0507,0655}

318106: {7886,9390}

318428: {1872,4548}

318594: {5091,5501}

318703: {0505,6814}

319722: {7009,7541}

320081: {0089,1201}

320549: {4780,9688}

321025: {0020,8594}

321026: {1045,1488}

321108: {2364,3963}

322286: {5390,9872}

322907: {5976,9894}

323025: {3082,5477}

323178: {4438,7411,9268}

323872: {5264,8601}

323973: {7651,9051}

324814: {4462,4521}

324885: {4116,8104}

326420: {5641,8345}

326585: {0703,3413}

326793: {7640,9369}

326886: {3632,7622}

327005: {7087,8412}

327241: {0013,4113}

327387: {2757,6279}

327406: {8469,9238}

327692: {0328,1158}

327856: {6037,7447}

327899: {2569,8404}

328022: {2068,8665}

328433: {3715,9685}

328441: {4541,5491}

328592: {1770,7600}

329117: {2725,3266,7959}

329142: {1846,7235}

329285: {0324,7893}

329773: {1510,6807}

329834: {3380,5873}

330434: {5197,8702}

330442: {0232,8274}

330690: {4111,6761}

331061: {3225,5929}

331358: {2540,7253}

331463: {1493,9185}

331571: {1174,7276}

331610: {8690,9273}

332045: {1192,9701}

332136: {2114,8049}

332481: {1728,5967}

332507: {4609,5093}

332627: {0126,2700}

333146: {2636,5860}

333450: {8609,9537}

333462: {5600,8478}

333663: {1050,7693}

333682: {8270,9353}

333998: {4034,7687}

334303: {3254,4714}

334617: {6586,7828}

334837: {2030,8091}

334914: {9034,9881}

335184: {3039,6080}

335216: {5066,9474}

335580: {4004,4864}

335618: {5891,9991}

335647: {4715,9359}

335648: {1060,3150}

335833: {0604,9269}

335867: {5145,8779}

336146: {7404,8354}

336846: {2783,4059}

337394: {0750,7595}

337524: {5159,9199}

338108: {4509,6866}

338157: {2741,4933}

338377: {1494,2094}

338420: {1515,3966}

338794: {9594,9845}

339154: {0743,9414}

339356: {1476,5817}

340009: {2933,8133}

340042: {2953,9957}

340097: {0172,1204}

340281: {5404,8419}

340472: {0060,3472}

340926: {0872,6788}

341131: {0237,6434,8154}

341157: {1810,9578}

341370: {5676,5786}

341506: {1432,6014}

341528: {3645,7689}

341902: {2203,6407}

341914: {5194,8521}

341983: {6118,7811}

342019: {2264,5218}

342233: {3949,5461}

342260: {0897,8605}

342394: {0260,8494}

342564: {4002,9173}

342630: {5527,8773}

342757: {3569,9032}

342821: {4799,5993}

343798: {7343,8491}

344003: {5961,7381}

344041: {2518,3260}

344251: {0102,3745}

344396: {1523,4810}

344780: {9627,9882}

345245: {1558,7972}

345278: {8163,9325}

345602: {4701,5555}

345933: {4788,9070}

345936: {1277,4166}

346134: {2839,8391}

346151: {0856,3654}

346219: {5495,5683}

346364: {4192,7639}

346769: {0587,1635,2374}

347036: {0559,8406}

347161: {8907,9741}

347522: {3605,3996}

347620: {2511,6244}

347740: {0579,8606}

347746: {4358,8878}

347775: {8741,9906}

347907: {2204,9640}

347925: {5423,6137}

348332: {6774,8667}

348762: {3488,6962}

348855: {0956,2340}

348911: {3646,9581}

349048: {3546,3744}

349073: {4179,8338}

349254: {3805,6726}

349471: {1047,4986}

349829: {6157,7860}

350183: {2142,6961,9708}

350308: {4130,6670}

350516: {4296,8527}

350569: {4060,9635}

350635: {1378,2927}

350684: {1261,7773}

351243: {1769,3536}

351326: {3121,7915}

351529: {2380,6571}

351561: {3911,5291}

351713: {2415,8585}

352134: {0692,1374}

352235: {5647,6629}

352294: {7046,8069}

352417: {0619,5419}

352438: {2439,8199}

352539: {6748,8705}

352694: {1180,7163}

353011: {2131,6621}

353082: {0174,4600}

353168: {1889,5682}

353239: {4050,9956}

353464: {2294,4966}

353828: {4931,7372}

353840: {0217,0907}

354455: {3776,6185}

355087: {4417,6577}

355188: {3510,5193}

355324: {0017,2318}

355402: {6057,7503}

355434: {3307,6790}

355805: {2138,3581}

355947: {1746,6743}

356094: {2159,6092}

356103: {2035,2615}

356255: {7001,8420}

356497: {1586,2339}

356516: {0066,0762}

356620: {3657,4174}

356900: {2055,5223}

356973: {8776,9103}

357223: {1687,7664}

358009: {7382,7497}

358487: {1366,4133}

359062: {1146,8147}

359220: {3660,8822}

359230: {6165,8191}

359616: {0633,6176}

360109: {2307,7362}

360826: {3455,7078}

361585: {4828,9217}

361678: {3837,7685}

362060: {0732,5850}

362094: {4434,8748}

362106: {2659,8340}

362129: {1302,2693,3550,9945}

362530: {2483,3015}

362580: {1281,5708}

362896: {4255,7722}

362924: {4744,9644}

363104: {0674,3672}

363222: {3484,7142}

363547: {2239,5260}

363885: {6291,7596}

363897: {2848,4773}

364027: {1035,8633}

364036: {7200,8926}

364503: {0589,5054}

364986: {0798,8765}

365010: {0005,8973}

365249: {5474,7459}

365443: {0073,7884}

365632: {1824,7237}

365776: {0071,8921}

365966: {0244,7492}

365968: {4984,5128}

365996: {7230,9404}

366225: {1300,3345}

366355: {9461,9915}

367072: {1481,5969}

367111: {2634,6306}

367217: {2393,2429}

367898: {4498,8180}

368443: {5085,7256}

368694: {5507,8283,9984}

368976: {6996,7062,7667}

369313: {2716,8640}

369495: {4545,7392}

369970: {2764,5011}

370814: {4601,6747}

370974: {4575,5613}

371553: {2804,6497}

372064: {6702,8361}

372108: {2949,7989}

372252: {1248,7907}

372311: {0050,5804}

372356: {4343,8399}

372357: {1716,7165}

372814: {6287,7363}

373523: {4530,8105}

373861: {3379,4697}

374797: {5925,8296}

374810: {1433,9562}

375824: {2284,6196}

376003: {1052,8083}

376138: {4294,7424}

376739: {9078,9973}

376760: {2051,9750}

376785: {0438,7605}

377455: {4277,5315}

378037: {2196,7421}

378355: {2938,9245}

378973: {2147,9852}

378984: {0276,6941}

379462: {0014,8562}

379612: {0680,5393}

379782: {1791,2266}

380544: {1328,8863}

381077: {7870,9296}

381177: {2894,7066}

381669: {0006,5820}

381849: {0597,5625}

382182: {3690,4675}

382940: {3346,8450}

383096: {4242,6254}

383242: {2584,7346}

383783: {3804,9176}

383870: {3557,9628}

384280: {1068,7269}

384385: {2436,4817}

384511: {3194,6645}

384649: {0881,6310}

385168: {4726,5116}

385543: {2545,8762}

386204: {9665,9773}

386294: {0727,1169}

387984: {5505,9448}

388202: {5985,8507}

389330: {1857,9447}

389349: {2841,5269}

389481: {2729,3998}

389795: {2367,4654}

389853: {1809,9849}

390037: {5162,5844}

390708: {0628,9706}

391278: {5899,7553}

391837: {2013,8526}

391929: {1713,3793}

392002: {2034,2872}

392518: {7118,9658}

393878: {5496,9517}

396142: {6936,8249}

396567: {7081,8211}

396886: {3938,8909}

397399: {0352,2680}

397503: {5059,9082}

397631: {1691,7111}

398347: {1367,5590}

398451: {2077,3116}

398583: {0687,9055}

398635: {4387,6361}

401346: {0266,4432}

402139: {5528,6893}

402315: {0936,7464}

403677: {3809,8263}

405493: {6027,6698}

407926: {0891,6640}

412908: {0278,3055}

413260: {0749,9602}

413732: {6654,7788}

414179: {8067,8580}

415732: {0870,6078}

416017: {0320,5720}

417139: {1126,9616}

417664: {4785,6195}

419623: {3402,3883}

420795: {1676,6722}

421861: {0786,1291}

423699: {3309,8888}

426750: {7638,9766}

433287: {1151,7375}

441637: {2651,2822}

452674: {3564,8663}

504659: {3418,3774}

514562: {0052,1787}

The red numbers in the summaries for each n-digit result has become a sequence: A360623.

Fenestron

The loud sound of a helicopter just before 10:30 p.m. last night got me to look out the window and, because of the unusual appearance of the tail, run to get my camera and take a photo from the front porch. The aircraft disappeared behind the apartment buildings on Weston Rd. — seemingly landing (in the vicinity of Weston's UP Express train station; I'm going to guess at the Toronto Paramedic Services lot). Coincidentally, a UP Express service alert appeared one-and-a-half hours later.

Lake effect

click to enlarge

It is sunny against a mostly blue sky backdrop outside but, as predicted, very cold. I did not even take Bodie for his walk this morning! My GOES 16 screen grab (above) shows snow streamers coming off the Great Lakes (left) with the prevailing northwesterly winds (below). The situation is even more pronounced off the coast of Maine (far right) where the lake effect is an ocean effect.

click to enlarge

Odd integer multiples via chess Knight moves

three: click to enlarge

five: click to enlarge

seven: click to enlarge

A million-digit Leyland prime (end of run)

manual distribution worksheet for 59536 primality tests

An hour ago I completed the primality check of 59536 Leyland-prime candidates that I started on 2 May 2022. My 27 May 2022 reality check explains why it took way longer (just short of nine months) than I had originally planned. Preceding the primality testing was another month (or so) sieving the original Leyland numbers file (so as to exclude divisibility by primes up to 2*10^11), so ten months altogether, now done.

What have I discovered? Of Leyland numbers with at least one million decimal digits, but fewer than one million one hundred decimal digits, there is only one prime. That prime was discovered by Gabor Levai long before I got to it. I saved all of my primality-test output where the 59536 entries are listed smallest to largest. If you want to see the one prime, search for "PRP".

The execution times vary wildly (due to processor circumstances) with an average of 9.45 hours per test. That would work out to 64 years if I hadn't been able to multi-process. I know now how to keep the execution times to 6 hours or less per test but that means running fewer processes per machine. Still, I might be able to shave a couple of months off the total time required for the next run.

A digit-spine sequence

Éric Angelini presented a proposal for three "digit-spine" sequences on his blog here, as well as to the MathFun community. I decided to take on the first one:

s = 1, 10, 2, 0, 3, 26, 9, 119, 532, 4, 6, 896, 118, 34, 15, ...

p = 2, 11, 2, 2, 3, 23, 7, 113, 523, 3, 5, 887, 113, 31, 13, ...

d = 1,  1, 0, 2, 0,  3, 2,   6,   9, 1, 1,   9,   5,  3,  2, ...

Our sought-after sequence is 's'. This is followed by 'p', a sequence of examples (for each, there might be a second such) of primes that are as close to the terms of 's' as possible. Finally 'd', the absolute differences between the respective  's' and 'p' values. Determining 's' is that it must be the lexicographically earliest sequence of distinct nonnegative integers such that its digit-spine (the sequential digits) as well as the digit-spine of 'd' are identical.

For example, the third 'd' being 0 is a consequence of the zero in 10, the second term of 's'. This forces the third term of 's' to be the smallest prime (as it had not already been used). And so on. There will always be integers in 'd' that inform our upcoming values in 's'. And the digits of those values get added to the growing end of our 'd' sequence.

So far, all of our 'd' values are single digits. But there will come a point when concatenating a digit with the next one in line allows for a smaller 's' term than what is available for the single digit. This first happens at term #1622 where a d = 1 dictates s = 1010. The next d digit is 0. Concatenating that 0 with the previous 1 gives us d = 10 at #1622 and this allows the smaller s = 897. This makes me want to know at which term the first three-digit d appears.

Maximilian Hasler helped Éric get the sequence into the OEIS. I have an indexed listing up to one million terms here.