In a recent three-and-a-half-hour video homage to John Conway, one of the participants, Siobhan Roberts, recalls Conway telling her that "time flies like an arrow; fruit flies like a banana." Roberts has written a biography of Conway. Of all the stories she might have used to illustrate the man's wit, this one struck me as odd — since of course the quote wasn't a Conway original.
Sometimes attributed to Groucho Marx, quote investigator "Garson O'Toole" (Gregory F. Sullivan) got it right in 2010 when he traced the core of the quotation to Anthony Oettinger, quoting from Oettinger's September 1966 Scientific American article touching on the subject of grammar by computer (time flies vs. fruit flies; the complication is mentioned as early as 1963 in the Harvard Alumni Bulletin). O'Toole: "By 1982 or before someone juxtaposed the sentences to yield a funny combination which was then assigned to Groucho Marx."
The April 1975 issue of Computers and People already had the juxtapositioning. Lawrence M. Clark wrote "Computer Programs that Understand Ordinary Natural Language" (pages 14-19, 23; page 14 reproduced here, quotation boxed in green). It gets better. Clark's three sentences appeared already in the November 1966 issue of Computers and Automation (different title, same publication). Neil Macdonald (a pseudonym for Edmund Berkeley) wrote a short "Research on Meaning in Programming Languages" (page 10, reproduced here). It is "peach" instead of "banana" but that is not as important as the date.
Sunday, May 24, 2020
Saturday, May 23, 2020
Where was Weston's Grammar School?
The Toronto Public Library has photo of a "Weston High School" located on the south side of King Street, west of Elm Street, not far from my parents' former house on Joseph Street. I had never known of a school having been at that location and that piqued my curiosity.
Cruickshank and Nason's "History of Weston" has the school "about a quarter-mile from the Main Street" which would put it closer to Rosemount Ave. than to Elm St. To resolve the location, I looked at a 1913 map that showed structures:
The red brick building in the middle of the above is my candidate for the Grammar School. Look at all the empty lots around it. To further convince myself:
Note that there is a slight forward protrusion of the left part of the building which matches the outline in the map. Finally, a 1924 map shows that the building is no longer there. Looking at the location today, one would see this.
Cruickshank and Nason's "History of Weston" has the school "about a quarter-mile from the Main Street" which would put it closer to Rosemount Ave. than to Elm St. To resolve the location, I looked at a 1913 map that showed structures:
The red brick building in the middle of the above is my candidate for the Grammar School. Look at all the empty lots around it. To further convince myself:
Note that there is a slight forward protrusion of the left part of the building which matches the outline in the map. Finally, a 1924 map shows that the building is no longer there. Looking at the location today, one would see this.
Saturday, May 16, 2020
What's an hour?
This morning a couple of ovenbirds crashed into our kitchen deck-door glass. The one on its side righted itself after a couple of minutes and they both just lay there in obvious shock. Here's a closeup of the upright one:
Catherine looked it up and said to just leave them for a few hours. And indeed, three hours later they were gone. This has happened before, twenty or more years ago (I am guessing), and — somewhat remarkably — the two birds that crashed into the door back then were also ovenbirds!
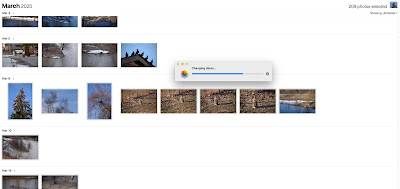
When I downloaded the photos for this article, I noticed that the time-stamp didn't seem right. I soon realized that I had forgotten to set the daylight-saving time option on my camera back on March 8. Which meant that I had 209 recent photos in my Apple Photos app that needed to be adjusted by one hour. Fortunately, Photos makes this easy. Unfortunately, the app hung ~70% through the process:
So I force-quit and relaunched the app to see what had been accomplished. I could see that some of the photos had added the hour but many had not. Worse, Photos had not gone through the 209 photos sequentially by date, but rather, somewhat haphazardly — a few each day. This is no doubt some sort of optimization procedure that utilizes multiple cores for speed gain (the same thing happens when one is importing photos from the camera). What Apple Photos did not realize is that my Mathematica was already utilizing all four cores on my Mac to calculate a ParallelTable. Perhaps this is why the application crashed.
Anyways, I now had to step through each day's photos and try to determine which ones had been adjusted and which had not. I had the camera's sequential photo numbers and the fact that many of the shots had been taken within minutes of each other to help me in this endeavour. However, for days (and parts of a day) where I had only taken one photo, this did not help. It took me another hour or so to step through my backup and check each photo's original time. Only later did I notice that the get-info on even the modified-time photos still showed the original time stamps.
All in all, it took me longer, I think, to correct all that Exif (when did they stop using all-caps?) data than it took those birds to recover. Moreover, I had to add an hour to the "posted" time on my Echo Beach post because I had originally cheated by back-timing that post to match the then-thought-to-be-correct photo time (to give it a more stream-of consciousness feel).
Thursday, May 14, 2020
Unfasten your safety belt
Two months ago we were strapped in for a year-or-two rollercoaster ride. Many bought into the lockdown as a necessary — but decidedly time-limited — mitigation. Two months at home seems to be about as much as the public can bear. It will be an interesting summer.
Sunday, May 10, 2020
Wanted
A virus with no sexual drive
Was wantin' to only survive.
But its number then grew
Exponential to two,
Which is odd since it wasn't alive.
Was wantin' to only survive.
But its number then grew
Exponential to two,
Which is odd since it wasn't alive.
 |
| with apologies to Randall Munroe |
Thursday, May 07, 2020
Ten random-start worlds in Rule 193
I first wrote about Rule 193 here, back in 2014. I decided to revisit the cellular automaton by setting up ten random-start evolutions:
Clicking on each panel will get you a larger version of that panel. Clicking on the numbers underneath each panel will get you the individual evolutions. The pictures are large: 14714 by 8508 pixels (~20 MB). Your browser will likely shrink each one to fit the browser window, so be sure to click/expand it to see all the glorious detail.
If you think of the downward-moving "lines" as particles, a lot of "physics" happens as the particles collide. How many different particles can you distinguish?
| 0 1 2 3 4 |
| 5 6 7 8 9 |
If you think of the downward-moving "lines" as particles, a lot of "physics" happens as the particles collide. How many different particles can you distinguish?
Saturday, May 02, 2020
Only eight
This typewritten table of the decimal expansions of powers of two up to 2^115 dates to when I was fourteen years old. My fascination then with powers of two almost certainly arose as a consequence of having encountered the wheat and chessboard problem. I would have calculated the numbers by hand and the typing layout suggests a slight obsession with presentation decorum, a handicap I've endured to the present day. The digit after the power is the digital root.
I recently had occasion to extend OEIS sequence A305942, the number of decimal powers of two having exactly n digits zero. For any given n, that number is fairly constant (on average a little over 33) but there is significant variation. For n up to 295000, I have found a zero-count as high as 62 and as low as 11. Checking other digits in the same range, I find a high of 65 and a low of 8 (see below). These extrema are outliers of course and statistics might suggest that we can find larger-than-65 and smaller-than-8 examples, if only we chart n large enough. But bear in mind that my current database of n up to 295000 is based on powers-of-two decimal expansions up to 2^10000000. It is not a fast computation.
This graph (click on it to get a better view) shows the number of occurrences (the blue points) of the digit 7 in decimal powers of two from 9100000 to 9240000. The green line represents the value 275923. Although (due to the size of the points and the thickness of the line) it may seem that there are dozens of points on the line, there are in fact only eight (at powers 9141747, 9143624, 9155434, 9163531, 9168298, 9171371, 9174454, and 9190491).
Subscribe to:
Posts (Atom)