I like to keep our grocery deliveries down to one-a-month which makes it difficult if ever they are out of something (or my personal shopper can't find it). One obvious remedy is to hoard more than a month's worth of staples so that out-of-stock items don't impact the unchanging (and somewhat inflexible) daily menu. Of course one can't really do that with milk and yogurt. Last summer I compensated by walking over to the nearby FreshCo for replacements. With the recent uptick in snow and Omicron, I perceived such a venture as too challenging. So last month I tried a second order, but from a different grocery delivery service. Even that was not able to procure me those big boxes of Bran Buds, so I resorted to asking Amazon for five of them (back on January 27). It was never going to be a fast delivery because (I think) they had to wait on Kellogg's but I still had a couple of big boxes and a couple of small ones on hand, so no problem. Then the Ambassador Bridge blockade made me worry a bit about it. The order arrived today! In the above photograph they are on the second shelf from the top.
Tuesday, February 22, 2022
Monday, February 21, 2022
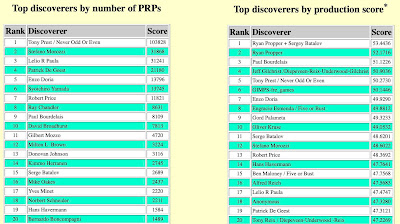
Number fourteen
This is a screen grab of today's probable-prime top-discoverers leaderboard that updates the one I posted on 7 May 2021. My production score now places me at #14. I am unlikely any time soon (if ever) to reach #13 and there is ample opportunity to be displaced downward by other people's efforts.* Of the 1584 PRPs noted, 1532 are Leyland primes. I reached my 1500th Leyland prime on 9 September 2021.
My worksheet (above) shows, at the bottom, the 74 cores currently working on Leyland interval L(302999,10) to L(303999,10) in which I have found so far 11 Leyland primes. It should be done in early March. After this I will do interval L(303999,10) to L(304999,10), taking me into May. This will then complete my attempt to find all Leyland primes in the interval L(299999,10) to L(304999,10). My thinking for what comes next has changed somewhat since the recent finds by the Levai brothers of five Leyland primes larger than 500000 decimal digits (at the bottom, here). I may to try to find a Leyland prime with one million (or more) decimal digits.
* Update (28 February 2022): Only one week later and I am again at #15 as Anonymous moved from #18 to #9.
Friday, February 18, 2022
80 on 80
An 80-year-old woman crossing the street died after being struck by an 80-year-old woman driving a Honda. Strikes me as a starting point for a science-fiction story or revenge drama.
Saturday, February 12, 2022
2022, for example
As we entered the current calendar year, James Propp (in a math-fun forum) noted a Dan McQuillan tweet on the embedding of the integer 2022 in its base-three representation:
2202220
The property is not the sole domain of 2022, but rather of a sequence of such integers wherein 2022 is the sixteenth term. James wanted to find out if this sequence was infinite. His argument had it that for length-d integers there should be slightly more than d solutions. Actual number of solutions for d up to 26 are:
3, 3, 6, 4, 4, 0, 0, 3, 3, 10, 0, 15, 14, 20, 8, 13, 20, 25, 9, 21, 14, 20, 23, 17, 8, 18.
That's 281 solutions altogether, thus far. Here are the last 18 (26-digit) solutions:
12120120221001100110120020101011000001200201100221210
[last updated 28 March 2022]