The unknown soldier

I have been cleaning up my primary iMac's virtual "desktop" for a week or so. One of the files thereon was a tabular listing of OEIS sequence A293355 up to term #291. When I submitted the sequence back in 2017, I included a listing of terms only up to #250, so clearly it was something I was extending at the time and hoping to extend even further. But other projects got in the way.

I had a look at term #291 and found that factordb had it fully factored in its database. If we have the full factorization of a sequence term, one may find the subsequent term by applying an algorithm to that factorization. If it's an easy factorization I can even automate the procedure in Mathematica and have it determine several terms at once. Unfortunately when one is trying to fully factorize a 90-plus-digit number, chances are that the second-largest factor is itself large (say, > 30 digits) and this makes it difficult for Mathematica to find in a reasonably short amount of time.

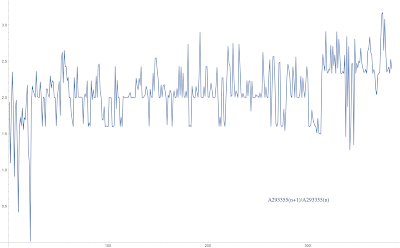
So I went back and forth (between Mathematica and factordb) yesterday trying to extend A293355 beyond term #291. Incredibly, every time I put a difficult-to-factor term into factordb it came back with the number fully factored! This was, clearly, no coincidence. Someone, three-or-so years ago, was also extending the sequence. Except that when they entered a term it did not come back fully factored. Instead they had the time-consuming task of factoring the number by other means. Whoever it was soldiered on, extending the sequence to term #384 which contained a 115-digit composite that my hero was apparently unable to resolve (unless, tragically, they succumbed in the battle). I submitted the updated, much larger "b-file" (an indexed tabular listing) to OEIS. The point of A293355 was to present an infinitary aliquot sequence (the one here starting with 6216) that seemed to evolve into monotonically increasing (never decreasing, by magnitude) terms. The actual term-by-term increases are much more interesting than the conjecture might suggest:

click to enlarge

Perhaps the sequence is just in some sort of "resonance" (for lack of a better word) that will eventually be disturbed by an unkind factorization — one that portends a much more chaotic future.

An abundance of additional terms (July 17): What goes up